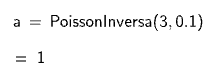Conocimiento pedagógico del eje probabilidad y estadística
Actualización 2024-08-07
Unidad 1 Profundización en Estadística y Probabidades
1.1 Variable Aleatoria
Una variable aleatoria proporciona un medio para describir los resultados experimentales utilizando valores numéricos, es decir, una variable aleatoria asocia un valor numérico a cada uno de los resultados experimentales. Una variable aleatoria puede ser discreta o continua, depende del tipo de valores numéricos que asuma. (Anderson. 2008, página 187).
- Una variable aleatoria se denomina discreta si asume un número finito de valores o una sucesión infinita de valores tales como \(0,1,2,\ldots\). Consideremos el siguiente experimento como ejemplo: un contador presenta el examen para certificarse como contador público. El examen tiene cuatro partes. Defina una variable aleatoria \(X\) como \(X = \text{número de partes del examen aprobadas}\). Esta es una variable aleatoria discreta porque puede tomar el número finito de valores \(0,1,2,3\,\,o \,\, 4\). Otros ejemplos se pueden observar en la siguiente tabla.
| Experimento | Variable aleatoria (\(X\)) | Valores posibles para la variable aleatoria |
|---|---|---|
| Llamar a cinco clientes | Número de clientes que hacen un pedido | \(0,1,2,3,4,5\) |
| Inspeccionar un envío de 50 radios | Número de radios que tienen algún defecto | \(0,1,2,…,49,50\) |
| Hacerse cargo de un restaurante durante el día | Número de clientes | \(0,1,2,3,…\) |
| Vender un automóvil | Sexo del cliente | 0 si el hombre, 1 si es mujer |
- Una variable aleatoria se denomina continua si puede tomar cualquier valor numéricos dentro de un intervalo. Los resultados experimentales basados en escalas de medición tales como tiempo, peso, distancia y temperatura puede ser descritos por variables aleatorias continuas. Consideremos el siguiente experimento como ejemplo: observar las llamadas telefónicas que llegan a la oficina de atención de una importante empresa de seguros. La variable aleatoria que interesa es
\(X=\) tiempo en minutos entre dos llamadas consecutivas. Esta variable aleatoria puede tomar cualquier valor en el intervalo \([0,\infty)\). En efecto, \(x\) puede tomar un número infinito de valores, entre los cuales se encuentra valores como \(1.25\) minutos \(3.4562\) minutos, \(4.33333\) minutos, etc. En la siguiente tabla aparecen otros ejemplos de variables aleatorias continuas.
| Experimento | Variable aleatoria (\(X\)) | Valores posibles para la variable aleatoria |
|---|---|---|
| Operar un banco | Tiempo en minutos entre la llegada de los clientes | \(x\geq 0\) |
| Llenar una lata de cerveza (capacidad máxima 350cc) | Cantidad en cc | \(0\leq x \leq 350\) |
| Llegada de Autobuses | Tiempo entre llegadas sucesivas de autobuses en una parada | \(x\geq 0\) |
| Probar un proceso químico nuevo | Temperatura a la que tiene lugar la reacción deseada (mín. 150 grados F, máx. 212 grados F) | \(150\leq x \leq 212\) |
1.2 Variables aleatorias discretas (v.a.d)
La distribución de probabilidad de una variable aleatoria discreta describe como se distribuyen las probabilidades entre los valores de la variable aleatoria. En el caso de una variable aleatoria discreta \(x\), la distribución de probabilidad está definida por una función de probabilidad o también llamada función de masa de probabilidad (fmp) (Devore, 2008, página 90).
1.2.1 Función de masa de probabilidad
Consideremos el siguiente ejemplo, una empresa acaba de adquirir cuatro impresoras láser y sea
\(X\) el número entre estas que requieren servicio durante el periodo de garantía. Los posibles valores de
\(X\) son entonces \(0, 1, 2, 3 \,\, y\,\, 4\). La distribución de probabilidad diría cómo está subdividida la probabilidad de uno entre los cinco posibles valores: ¿cuánta probabilidad está asociada con el valor 0 de \(X\), cuánta está adjudicada con 1 de \(X\) y así sucesivamente?. Se utiliza la siguiente notación para las probabilidades:
\(p(0) =\) la probabilidad del valor 0 de \(X = P(X=0)\)
\(p(1) =\) la probabilidad del valor 1 de \(X = P(X=1)\)
y así sucesivamente. En general, \(p(x)\) denotará la probabilidad asignada al valor de \(x\).
Ejemplo: Una cierta gasolinera tiene seis bombas. Sea
\(X\) el número de bombas que están bajo servicio a una hora particular del día. Suponga que la distribución de probabilidad de \(X\) es como se detalla en la siguiente tabla; la primera fila de la tabla contiene los posibles valores de \(X\) y la segunda la probabilidad de dicho valor.
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| \(p(x)\) | 0.05 | 0.1 | 0.15 | 0.25 | 0.2 | 0.15 | 0.1 |
Ejemplo 01, la probabilidad de que a lo más dos bombas estén en servicio es
\[\begin{equation} \notag \begin{split} P(X\leq 2) &= P(X = 0 \text{ o } 1 \text{ o } 2) \\ & = p(0) + p(1) + p(2) \\ & = 0.05 + 0.1 + 0.15 = 0.3 \end{split} \end{equation}\]
Ejemplo 02, la probabilidad de que estén entre 2 y 4 bombas (inclusive) en servicio
\[\begin{equation} \notag \begin{split} P(2\leq X\leq 4) &= P(X = 2 \text{ o } 3 \text{ o } 4)\\ & = p(2) + p(3) + p(4) \\ & = 0.15 + 0.25 + 0.2 = 0.6 \end{split} \end{equation}\]
La situación anterior graficamente queda
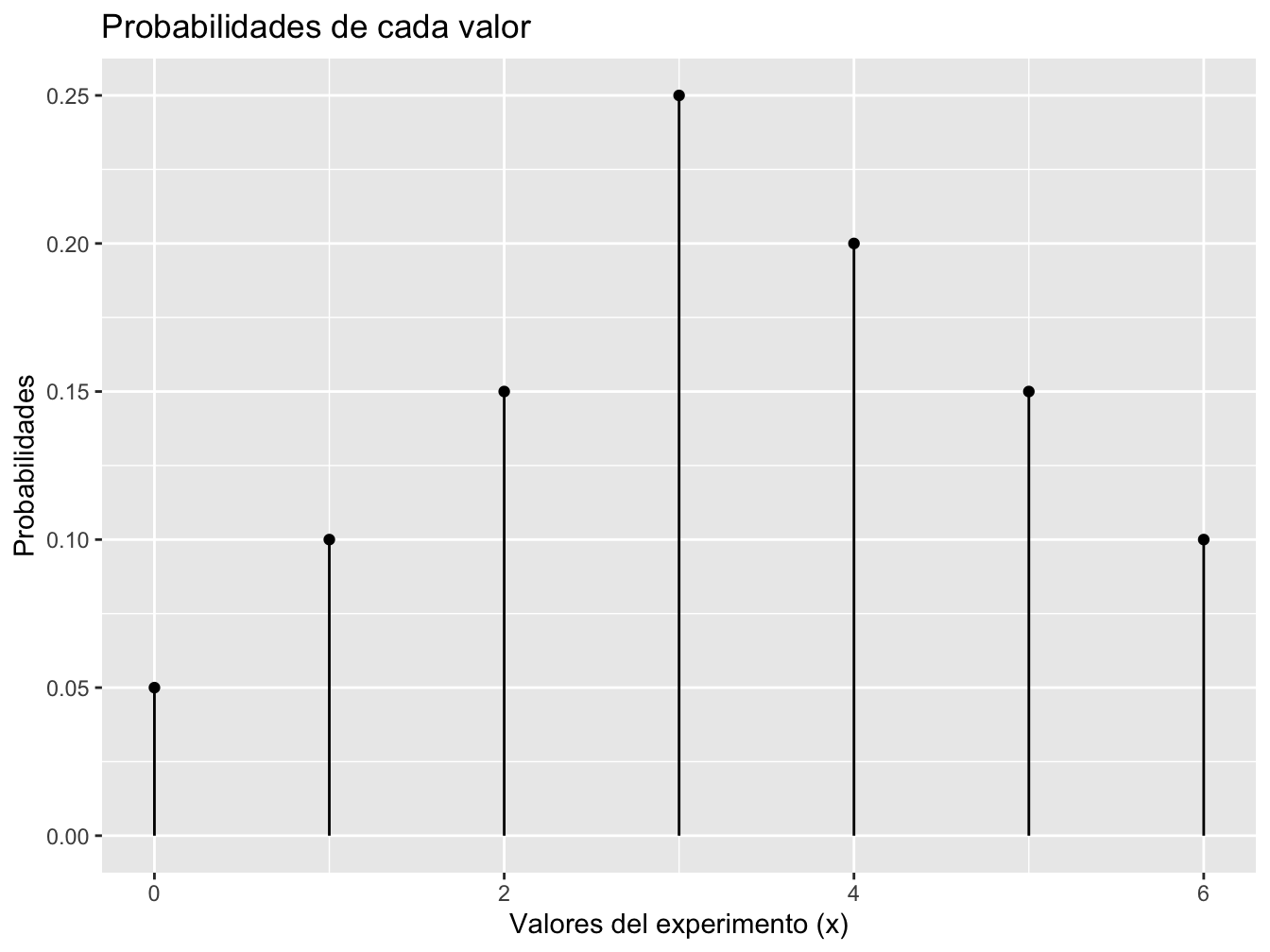
Figure 1.1: Función de masa
Cabe mencionar que cualquier función de masa de probabilidad requiere cumplir las siguientes condiciones
- \(p(x) > 0, \forall x \in X\)
- \(\displaystyle\sum_{\text{todas las x posibles}} p(x) = 1\)
Ejercicio: Seis lotes de componentes están listos para ser enviados por un proveedor. El número de componentes defectuosos en cada lote es como sigue:
| Lote | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| N° articulos defectusos | 0 | 2 | 0 | 1 | 2 | 0 |
Uno de estos lotes tiene que ser seleccionado al azar para ser enviado a un cliente particular. Sea \(X\) el número de componentes defectuosos en el lote seleccionado. Los tres posibles valores de \(X\) son 0, 1 y 2.
Determine la probabilidad para cada uno de los valores de
\(X\). Interprete.Verifique las condiciones de la función de masa de probabilidad asociada al experimento.
Grafique la función de masa asociada
Ejercicio: Una empresa de ventas en línea dispone de seis líneas telefónicas. Sea \(X\) el número de líneas en uso en un tiempo epsecificado. Suponga que la función de masa de probabilidad de \(X\) es la que se da en la tabla adjunta.
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| \(p(x)\) | 0.1 | 0.15 | 0.2 | 0.25 | 0.2 | 0.06 | 0.04 |
Grafique la función de masa asociada, y luego calcule la probabilidad de cada uno de los siguientes eventos.
Cuando mucho tres líneas están en uso.
Menos de tres líneas están en uso.
Por lo menos tres líneas están en uso.
Entre dos y cinco líneas, inclusive, están en uso.
Entre dos y cuatro líneas, inclusive, no está en uso.
Por lo menos cuatro líneas no están en uso.
1.2.2 Función de distribución acumulada
Para algún valor fijo de \(x\), a menudo se desea calcular la probabilidad de que el valor observado de \(X\) sea cuando mucho \(x\) \((X \leq x)\). Por ejemplo, consideremos la siguiente función de masa.
\[\begin{equation} \notag \begin{split} P(X = x) = p(x) = \left\lbrace \begin{matrix} 0.5 & x = 0\\ 0.167 & x = 1\\ 0.333 & x = 2\\ 0 & \text{en otro caso}\\ \end{matrix} \right. \end{split} \end{equation}\]
La probabilidad de que \(X\) sea a lo más 1 es entonces
\[P(X \leq 1) = p(0) + p(1) = 0.5 + 0.167 = 0.667\]
Asimismo,
\[P(X \leq 0) = P(X = 0) = 0.5\]
La función de distribución acumulada (fda) \(F(x)\) de una variable aleatoria discreta \(X\) con función de masa de probabilidad \(P(X=x)\) se define como
\[\begin{equation} F(x) = P(X\leq x) =\displaystyle\sum_{y\leq x}P(X=y) \end{equation}\]
Para cualquier número \(x\), \(F(X)\) es la probabilidad de que el valor observado de \(X\) será cuando mucho (como máximo) \(x\). (Devore, 2008, página 95)
Ejemplo: Consideremos un grupo de cinco donadores de sangre potenciales, \(a\), \(b\), \(c\), \(d\) y \(e\), de los cuales solo \(a\) y \(b\) tienen sangre tipo O+. Se determinará en orden aleatorio el tipo de sangre con cinco muestras, una de cada individuo hasta que se identifique un individuo O+. Sea la variable aleatoria \(Y =\) el número de exámenes de sangre para identificar un individuo O+. Entonces la función de masa de probabilidad de \(Y\) es
| \(y\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(p(y)\) | 0.4 | 0.3 | 0.2 | 0.1 |
Para determinar la función de distribución acumulada \(F(Y)\), lo primero es determinar el valor de \(F(Y)\) para cada uno de los valores posibles del conjunto \((1,2,3,4)\):
\[\begin{equation} \notag \begin{split} F(1) &= P(Y\leq 1) = P(Y = 1) = p(1) = 0.4\\ F(2) &= P(Y\leq 2) = P(Y = 1 \text{ o } 2) = p(1) + p(2) = 0.7\\ F(3) &= P(Y\leq 3) = P(Y = 1 \text{ o } 2 \text{ o } 3) = p(1) + p(2) + p(3) = 0.9\\ F(4) &= P(Y\leq 4) = P(Y = 1 \text{ o } 2 \text{ o } 3 \text{ o } 4) = p(1) + p(2) + p(3) + p(4) = 1\\ \end{split} \end{equation}\]
Ahora con cualquier otro número \(y\), \(F(Y)\) será igual al valor de \(F\) con el valor más próximo posible de \(Y\) a la izquierda de \(y\). Por ejemplo, \(F(2.7)=P(Y≤2.7)=p(Y≤2)=0.7\) y \(F(3.9999)=F(3)=0.9\). La función de distribución acumulativa es por lo tanto
\[\begin{equation} \notag \begin{split} F(y) = \left\lbrace \begin{matrix} 0 & \text{si } & y < 1\\ 0.4 & \text{si } & 1\leq y < 2\\ 0.7 & \text{si } & 2\leq y < 3\\ 0.9 & \text{si } & 3\leq y < 4\\ 1 & \text{si } & y\geq 4\\ \end{matrix} \right. \end{split} \end{equation}\]
La siguiente figura muestra la gráfica de \(F(y)\).
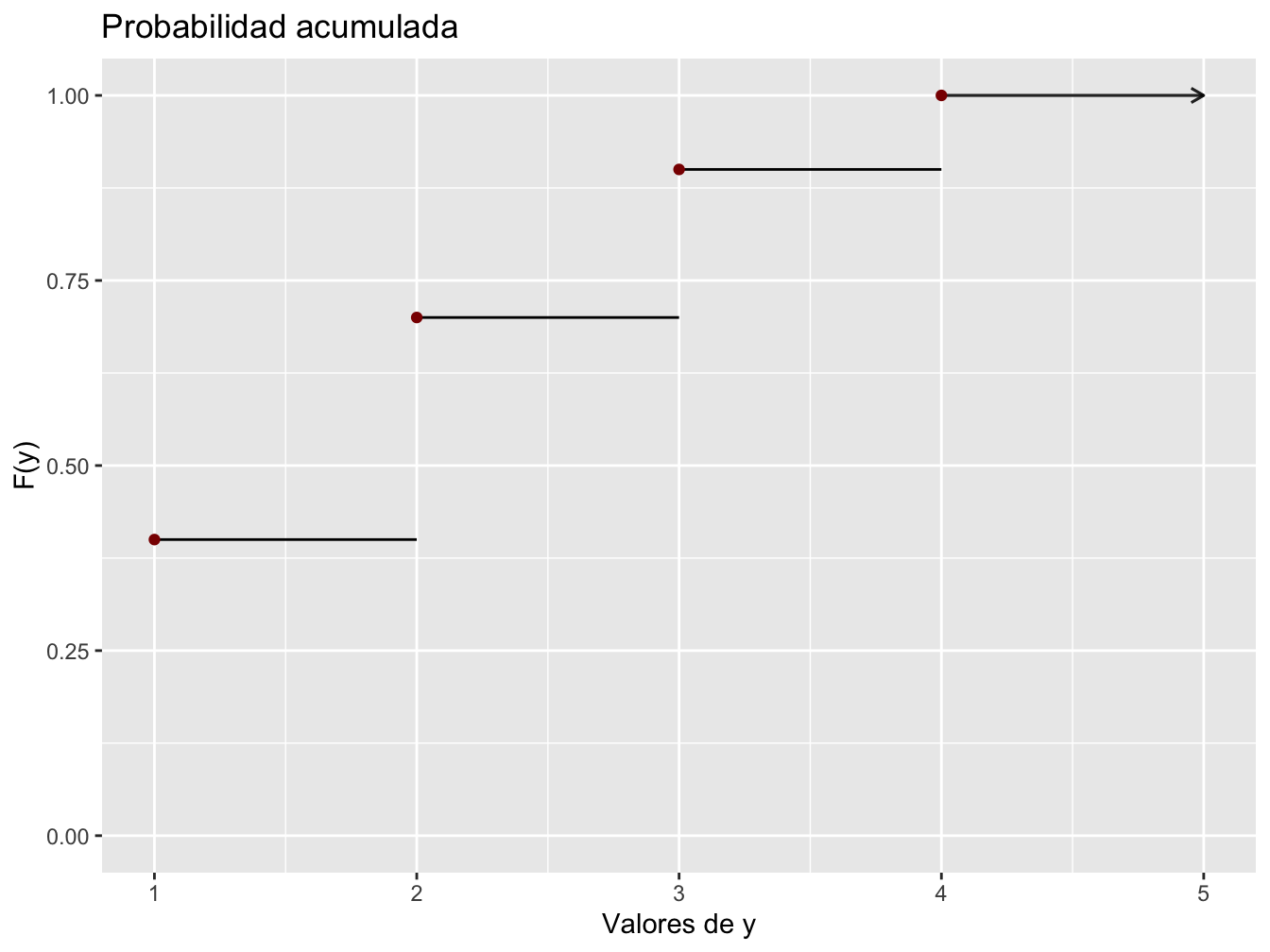
Figure 1.2: Función de distribución acumulada
Para una variable aleatorio discreta \(X\), la gráfica de \(F(X)\) mostrará un saltó con cada valor posible de \(X\) y será plana entre los valores posibles. Tal gráfica se conoce como función escalonada
Una propiedad que surge de la función de distribución acumulada es que, para dos números cualesquiera \(a\) y \(b\) con \(a≤b\)
\[\begin{equation} P(a\leq X \leq b) = P(X \leq b) - P(X < a) \end{equation}\]
En caso de que se desee calcular \(P(a < X \leq b)\), la propiedad sería
\[\begin{equation} P(a < X \leq b) = P(X \leq b) - P(X \leq a) = F(a) - F(b) \end{equation}\]
Ejercicio: Con respecto al ejercicio “Una empresa de ventas en línea” y calcule y trace la gráfica de la función de distribución acumulada \(F(X)\). Luego, utilícela para calcular las probabilidades de los eventos dados en los ítem a. y d. de dicho problema. Además, grafique la función de distribución acumulada.
Ejercicio: Una organización de protección al consumidor que habitualmente evalúa automóviles nuevos reporta el número de defectos importantes encontrados en un carro seleccionado al azar de cierto tipo. La función de distribución acumulativa de \(Y\) es la siguiente.
\[\begin{equation} \notag \begin{split} F(y) = \left\lbrace \begin{matrix} 0 & \text{si } & y < 0\\ 0.06 & \text{si } & 0\leq y < 1\\ 0.19 & \text{si } & 1\leq y < 2\\ 0.39 & \text{si } & 2\leq y < 3\\ 0.67 & \text{si } & 3\leq y < 4\\ 0.92 & \text{si } & 4\leq y < 5\\ 0.97 & \text{si } & 5\leq y < 6\\ 1 & \text{si } & y\geq 6\\ \end{matrix} \right. \end{split} \end{equation}\]
- Calcule las siguientes probabilidades directamente con la función de distribución acumulada:
- \(p(2)\), es decir, \(P(Y=2)\)
- \(P(Y>3)\)
- \(P(2\leq Y\leq5)\)
- \(P(2< Y<5)\)
- ¿Cuál es la función de masa de probabilidad de \(Y\)? Grafique la función de masa de probabilidad, y la función de distribución acumulada.
Ejercicio: En una fábrica de productos electrónicos, se sabe que la probabilidad de que un artículo sea defectuoso sigue una distribución de probabilidad de masa con los siguientes valores:
| Número de defectos | Probabilidad |
|---|---|
| 0 | 0.50 |
| 1 | 0.30 |
| 2 | 0.02 |
| 3 | 0.08 |
| 4 | 0.10 |
- Determine la función de masa de probabilidad.
- Determine la función de distribución acumulada.
- Si se selecciona un artículo al azar. Utilizando la función de distribución acumulada calcule:
- La probabilidad de que tenga cuando mucho de 2 defectos.
- La probabilidad de que tenga más de 0.4 defectos.
- La probabilidad de que tenga entre 1 y 4 defectos.
- La probabilidad de que tenga cuando menos 2.7 defectos.
1.2.3 Distribuciones
A continuación, se dan a conocer algunas de las distribución de probabilidad discreta más utilizadas. Cabe mencionar, que existen muchas otras distribuciones, por lo que se invita al estudiante a informarse de ellas en caso de que lo requiera.
1.2.3.1 Bernoulli
La distribución Bernoulli es una distribución de probabilidad discreta que describe el resultado de un experimento de ensayo único que puede tener dos posibles resultados, a menudo etiquetados como éxito y fracaso, con una probabilidad de éxito de \(p\) y una probabilidad de fracaso de \(q=1−p\). La función de masa de probabilidad de la distribución Bernoulli está dada por:
\[\begin{equation} P(X = x) = p^x(1-p)^{1-x} \end{equation}\]
donde \(x\) puede tomar únicamente los valores de 0 y 1 (Larsen & Marx, 2017, página 105).
Ejemplo: En un experimento de lanzamiento de moneda, se puede modelar la probabilidad de obtener cara como una distribución Bernoulli. En este caso, si se define “éxito” como obtener cara y “fracaso” como obtener sello, entonces la probabilidad de éxito es \(p=0.5\) y la probabilidad de fracaso es \(q=1−p=0.5\). Entonces, la distribución Bernoulli para este experimento estaría dada por:
\(P(\text{Obtener cara})=p=0.5\)
\(P(\text{Obtener sello})=q=0.5\)
Ejemplo: En una campaña publicitaria en línea, se puede modelar la probabilidad de que un usuario haga clic en un anuncio como una distribución Bernoulli. En este caso, si se define “éxito” como un usuario que hace clic en el anuncio y “fracaso” como un usuario que no hace clic, entonces la probabilidad de éxito es p y la probabilidad de fracaso es \(q=1−p\). Supongamos que la probabilidad de que un usuario haga clic en el anuncio es del 10%, es decir, \(p=0.1\). Entonces, la distribución Bernoulli para este experimento estaría dada por:
\(P(\text{Hacer clic en el anuncio}) = p = 0.1\)
\(P(\text{No hacer clic en el anuncio}) = p = 0.9\)
1.2.3.2 Binomial
La distribución de probabilidad binomial es una distribución de probabilidad que tiene muchas aplicaciones. Está relacionada con un experimento de pasos múltiples al que se llama experimento binomial (Anderson et al., 2008, paǵina 200).
Un experimento binomial tiene las siguientes cuatro propiedades.
- El experimento consiste en una serie de \(n\) ensayos idénticos.
- En cada ensayo hay dos resultados posibles. A uno de estos resultados se le llama éxito y al otro se le llama fracaso.
- La probabilidad de éxito, que se denota \(p\), no cambia de un ensayo a otro. Por ende, la probabilidad de fracaso, que se denota \(1−p\), tampoco cambia de un ensayo a otro.
- Los ensayos son independientes.
Si se presentan las propiedades \(2\), \(3\) y \(4\), se dice que los ensayos son generados por un proceso de Bernoulli. Si, además, se presenta la propiedad \(1\), se trata de un experimento binomial.
Ejemplo: Considere el experimento que consiste en lanzar una moneda cinco veces y observar si es cara o sello. Suponga que se desea contar el número de caras que aparecen en los cinco lanzamientos. ¿Presenta este experimento las propiedades de un experimento binomial? ¿Cuál es la variable aleatoria que interesa? Observe que:
- El experimento consiste en cinco ensayos idénticos; cada ensayo consiste en lanzar una moneda.
- En cada ensayo hay dos resultados posibles: cara o sello. Se puede considerar cara como éxito y sello como fracaso.
- La probabilidad de éxito y la probabilidad de fracaso son iguales en todos los ensayos, siendo \(p=0.5\) y \(1−p=0.5\).
- Los ensayos o lanzamientos son independientes porque al resultado de un ensayo no afecta a lo que pase en los otros ensayos o lanzamientos.
Por tanto, se satisfacen las propiedades de un experimento binomial. La variable aleatoria que interesa es \(X= \text{número de caras que aparecen en cinco ensayos}\). En este caso, \(X\) puede tomar los valores \(0\), \(1\), \(2\), \(3\), \(4\) o \(5\).
La función de masa de probabilidad de la distribución Binomial está dada por:
\[\begin{equation} P(X = x) = \binom{n}{x}p^x(1-p)^{n-x} \end{equation}\]
Donde,
\[\begin{equation} \notag \begin{split} P(X = x) &= \text{probabilidad de } x \text{ éxitos en } n \text{ ensayos}\\ n &= \text{ número de ensayos}\\ \binom{n}{x} &= \dfrac{n!}{x!(n-x)!}\\ p &= \text{probabilidad de un éxito en cualquiera de los ensayos}\\ 1 - p &= \text{probabilidad de un fracaso en cualquiera de los ensayos}\\ \end{split} \end{equation}\]
Ejemplo: Considere una distribución Binomial con \(n=7\) y \(p=0.2\).
Escriba la función de masa de probabilidad asociada.
Calcule \(p(4)\)
- Usando R
dbinom(
x = 4, # Valor de X para el cual se desea calcular la probabilidad
size = 7, # Cantidad de ensayos
prob = 0.2, # Probabilidad de éxito
)## [1] 0.028672- Usando GeoGebra:
- Usando Excel
Por lo tanto, la probabilidad de obtener 4 resultados exitosos de 7 ensayos es de 0.028672.
- Calcule \(P(X\leq 2)\)
Por defecto, R considera que las probabilidades acumuladas son del tipo \(P(X≤x)\), tal como se presenta en este enunciado.
pbinom(
q = 2, # Se consideran valores MENORES o iguales a 2
size = 7, # Cantidad de ensayos
prob = 0.2, # Probabilidad de éxito
)## [1] 0.851968Por lo tanto, la probabilidad de obtener 2 o menos resultados exitosos de 7 ensayos es de 0.85.
- Calcule \(P(X<5)\).
En este caso antes de calcular en la probabilidad en R, se debe transformar la expresión a la forma \(P(X≤x)\). Ya que estamos trabajando con eventos discretos, tenemos que
\(P(X<5)=P(X≤4)\) Luego, esta probabilidad la podemos calcular en R de la siguiente manera.
pbinom(
q = 4, # Se consideran valores MENORES o iguales a 4
size = 7, # Cantidad de ensayos
prob = 0.2, # Probabilidad de éxito
)## [1] 0.995328Por lo tanto, la probabilidad de obtener menos de 5 resultados exitosos de 7 ensayos es de 0.99.
- Calcule \(P(X>1)\) R incluye un comando para aquellos casos en los que el signo de desigualdad estricto es del tipo mayor.
pbinom(
q = 1, # Se consideran valores MAYORES o iguales a 1
size = 7, # Cantidad de ensayos
prob = 0.2, # Probabilidad de éxito
lower.tail = FALSE # En caso de que se tenga el signo mayor estricto
)## [1] 0.4232832- Calcule \(P(X≥1)\).
Para aquellos casos en que se tenga el signo de mayor igual \((≥)\), lo más más recomendable es transformar la expresión a estricto \((>)\) para así utilizar un código similar al del ejemplo d. Ya que estamos trabajando con eventos discretos, tenemos que
\(P(X≥1)=P(X>0)\)
Luego, esta probabilidad la podemos calcular en R de la siguiente manera.
pbinom(
q = 0, # Se consideran valores MAYORES a 0
size = 7, # Cantidad de ensayos
prob = 0.2, # Probabilidad de éxito
lower.tail = FALSE # En caso de que se tenga el signo mayor estricto
)## [1] 0.7902848- ¿Para que valor de\(x\), \(P(X≤x)=0.6\)? Despejar esta ecuación puede llegar a ser engorroso. Sin embargo, R posee un argumento para determinar estos valores. Para el calculo se debe usar el prefijo q seguido de la abreviatura de la distribución discreta, en este caso la abreviatura de la distribución Binomial es binom.
qbinom(
p = 0.6, # Valor resultante de la probabilidad
size = 7, # Cantidad de ensayos
prob = 0.2, # Probabilidad de éxito
)## [1] 2- Usando GeoGebra:

- Usando Excel

Por lo tanto, para \(x=2\), la probabilidad de obtener a lo más \(x\) resultados exitosos es de 0.6.
Ejemplo: Un acusado va a ser declarado inocente o culpable por un jurado popular. Para ser condenado es necesario que al menos 7 personas de las 10 del jurado voten culpable. Dado que en los programas de televisión ya han dado muchos detalles del caso, los miembros del jurado están atendiendo o leyendo el diario en vez de escuchar al fiscal y al abogado, porque van a decidir tirando una moneda al aire. ¿Cuál es la probabilidad de que el acusado sea declarado inocente?
La probabilidad de éxito (inocencia) es de \(p=0.5\). Sea \(X\) el número éxitos (votos de inocencia) en 10 ensayos (votos del jurado). Entonces, la probabilidad de ser declarado inocente esta dada por la siguiente expresión.
\[P(X \geq 4) = \sum_{k=4}^{10} \binom{10}{k} 0.5^{k}(1-0.5)^{10-k} = 0.82,\text{ o}\]
Antes de realizar el cálculo en R lo recomendable es transformar la expresión para utilizar el comando adecuado. En este caso, la expresión es:
\[P(X\geq 4) = P(X > 3)\]
pbinom(
q = 3, # Se consideran valores MAYORES o iguales a 3 (es decir, mayor o igual a 4)
size = 10, # Cantidad de ensayos
prob = 0.5, # Probabilidad de éxito
lower.tail = FALSE # TRUE: menor igual, FALSE: mayor estricto
)## [1] 0.828125- Usando GeoGebra:
- Usando Excel
Por otro lado, la probabilidad \(P(X\geq 4)\) puede ser escrita como \(1 - P(X \leq 3)\)
\[1 - P(X \leq 3) = \sum_{k=0}^{3} \binom{10}{k} 0.5^{k}(1-0.5)^{10-k} = 0.82\]
Es posible calcular esta expresión en R de la siguiente manera.
1 - pbinom(
q = 3, # Se consideran valores MENORES o iguales a 3
size = 10, # Cantidad de ensayos
prob = 0.5 # Probabilidad de éxito
)## [1] 0.828125Por lo tanto, la probabilidad de que el acusado sea declarado inocente es de 0.82.
Ejercicios propuestos
Ejercicio 01: En una planta de revisión técnica, resulta rechazado el 42% de los vehículos livianos. En la primera media hora de un día cualquiera se alcanzan a revisar 9 vehículos.
- ¿cuál es la probabilidad de que más de 3 sean rechazados?
- ¿cuál es la probabilidad de que a lo más 5 sean rechazados?
- ¿cuál es la probabilidad de que menos de 2 sean rechazados?
- ¿cuál es la probabilidad de no se rechacen todos los vehículos?
Ejercicio 02: Se sabe que la probabilidad de que una empresa no pase la revisión de fraude fiscal es de 0.21. De las siguientes 345 empresas que se revisan en búsqueda de fraude fiscal, calcule la probabilidad de que cuando mucho 85 empresas no aprueben la revisión.
Ejercicio 03:Un banco sabe que el 8% de sus clientes no pagan a tiempo sus tarjetas de crédito. Si el banco emite 2500 tarjetas de crédito,
- ¿Cuál es la probabilidad de que al menos 200 de ellas pertenezcan a clientes que no pagan a tiempo?
- ¿Qué pasaría con la probabilidad de que al menos 200 de las tarjetas de crédito pertenezcan a clientes que no pagan a tiempo si la tasa de incumplimiento del banco aumenta al 9.2%?
- ¿Cuál es la probabilidad de que exactamente 250 de las tarjetas de crédito pertenezcan a clientes que no pagan a tiempo?
- ¿Cuál es la probabilidad de que cuando mucho 210 de ellas pertenezcan a clientes que no pagan a tiempo?
1.2.3.3 Poisson
Una variable aleatoria discreta que se suele usar para estimar el número de veces que sucede un hecho determinado (ocurrencias) en un intervalo de tiempo o de espacio. Por ejemplo, el número de reparaciones en un autopista o número de fugas en un tubería. Si se satisfacen las siguientes condiciones, el número de ocurrencias es una variable aleatoria discreta definida por la distribución de probabilidad de Poisson (Anderson et al., 2008, página 211).
- La probabilidad de ocurrencia es la misma para cualesquiera dos intervalos de la misma magnitud.
- La ocurrencia o no-ocurrencia en cualquier intervalo es independiente de la ocurrencia o no-ocurrencia en cualquier otro intervalo.
La función de masa de probabilidad de Poisson se define mediante la ecuación
\[\begin{equation} P(X = x) = \dfrac{\lambda^xe^{-\lambda}}{x!} \end{equation}\]
en donde
\[\begin{equation} \notag \begin{split} P(X = x) &= \text{probabilidad de } x \text{ ocurrencias en un intervalo de tiempo}\\ \lambda &= \text{ tasa de ocurrencias en un intervalo}\\ e &\approx 2.71828\\ \end{split} \end{equation}\]
Es importante observar, que el número de ocurrencias de \(x\), no tiene límite superior. Esta es un variable aleatoria discreta que toma los valores de una sucesión infinita de números \((x=0,1,2,3,4,…)\)
Ejemplo: Considere una distribución Poisson con \(λ=3\)
- Escriba la función de probabilidad asociada.
\[\begin{equation} \notag P(X=x) = \dfrac{3^xe^{-3}}{x!} \end{equation}\]
- Calcule \(p(2)\)
dpois(
x = 2, # Valor de X para el cual se desea calcular la probabilidad
lambda = 3 # Tasa de ocurrencia por unidad de tiempo o espacio
)## [1] 0.2240418- Usando GeoGebra:
- Usando Excel
Por lo tanto, teniendo una tasa de 3 por unidad de tiempo, la probabilidad de que ocurran dos sucesos es de 0.22.
- Calcule \(P(X)≤3)\)
ppois(
q = 3, # Valor de X para el cual se desea calcular la probabilidad
lambda = 3 # Tasa de ocurrencia por unidad de tiempo o espacio
)## [1] 0.6472319- Usando GeoGebra:
- Usando Excel
Por lo tanto, teniendo una tasa de 3 por unidad de tiempo, la probabilidad de que ocurran a lo más tres sucesos es de 0.64.
- Calcule \(P(X < 2)\)
ppois(
q = 1, # Valor de X para el cual se desea calcular la probabilidad
lambda = 3 # Tasa de ocurrencia por unidad de tiempo o espacio
)## [1] 0.1991483- Usando GeoGebra:
- Usando Excel
- Calcule \(P(X > 2)\)
ppois(
q = 2, # Valor de X para el cual se desea calcular la probabilidad
lambda = 3, # Tasa de ocurrencia por unidad de tiempo o espacio
lower.tail = FALSE # En caso de que se tenga el signo mayor estricto
)## [1] 0.5768099- Usando GeoGebra:
- Usando Excel
Por lo tanto, teniendo una tasa de 3 por unidad de tiempo, la probabilidad de que ocurran más de dos sucesos es de 0.58.
- Calcule \(P(X\geq 5)\)
ppois(
q = 4, # Valor de X para el cual se desea calcular la probabilidad
lambda = 3, # Tasa de ocurrencia por unidad de tiempo o espacio
lower.tail = FALSE # En caso de que se tenga el signo mayor estricto
)## [1] 0.1847368- Usando GeoGebra:
- Usando Excel
Por lo tanto, teniendo una tasa de 3 por unidad de tiempo, la probabilidad de que ocurran al menos cinco sucesos es de 0.18.
- Calcule \(P(X\leq x) = 0.1\)
qpois(
p = 0.1, # Valor resultante de la probabilidad
lambda = 3 # Tasa de ocurrencia por unidad de tiempo o espacio
)## [1] 1- Usando GeoGebra:
Por lo tanto, para \(x=1\), la probabilidad de que ocurran a los más \(x\) sucesos es de 0.1, considerando una tasa de 3 por unidad de tiempo.
Ejemplo: Por un paradero pasan los buses de la línea \(A\) a una razón de 12 por hora y en forma independiente pasan los buses de la línea \(B\) a razón de 10 por hora. Un inspector observa la pasada de buses por el paradero.
- ¿Cuál es la probabilidad de que en los primeros 10 minutos no pasen buses de la línea \(A\)?
La tasa de llegada de buses de la línea \(A\) es de 12 por hora, por lo tanto, la tasa de llegada en 10 minutos es de 2 buses \((12/60\cdot 10=2)\). La probabilidad de que no pase ningún bus en esos 10 minutos esta dada por \(P(X=0)\). En R:
dpois(
x = 0, # Valor de X para el cual se desea calcular la probabilidad
lambda = 2 # Tasa de ocurrencia por unidad de tiempo o espacio
)## [1] 0.1353353Por lo tanto, la probabilidad de que en los primeros 10 minutos no pase ningún bus de la línea \(A\) es de aproximadamente 0.13.
- ¿Cuál es la probabilidad de que en los primeros 8 minutos pasen menos de 3 buses de la línea
\(B\)?
La tasa de llegada en 8 minutos es de aproximadamente 1.333 buses \((10/60\cdot 8=1.333)\) . Entonces, la probabilidad de que pasen menos de 3 buses de la línea \(B\) en esos 8 minutos esta dada por \(P(X<3)=P(X≤2)\). En R:
ppois(
q = 2, # Valor de X para el cual se desea calcular la probabilidad
lambda = 1.333 # Tasa de ocurrencia por unidad de tiempo o espacio
)## [1] 0.8494467La probabilidad de que en los primeros 8 minutos pasen menos de 3 buses de la línea \(B\) es de aproximadamente 0.84.
Ejercicios propuestos
Ejercicio 01: Una compañía de seguros tiene un promedio de 4 reclamaciones de seguros de automóviles por día.
¿Cuál es la probabilidad de que la compañía de seguros reciba menos de 3 reclamaciones en un día?
¿Cuál es la probabilidad de que la compañía de seguros reciba como máximo 7 reclamaciones en un día?
¿Cuál es la probabilidad de que la compañía de seguros reciba cuando menos 2 reclamaciones en un día?
¿Cuál es la probabilidad de que la compañía de seguros reciba entre 2 y 5 reclamaciones en un día?
¿Cuál es la probabilidad de que la compañía de seguros reciba de 1 a 3 reclamaciones en un día?
Ejercicio 02: Un banco recibe en promedio 2 solicitudes de préstamos hipotecarios por hora.
¿Cuál es la probabilidad de que el banco reciba exactamente 3 solicitudes de préstamo hipotecario en un periodo de 90 minutos?
¿Cuál es la probabilidad de que el banco reciba más de 4 solicitudes de préstamo hipotecario en un periodo de 80 minutos?
¿Cuál es la probabilidad de que el banco reciba cuando mucho 5 solicitudes de préstamo hipotecario en un periodo de dos horas?
Ejercicio 03: Un laboratorio farmacéutico encarga una encuesta para estimar el consumo de cierto medicamento que, elabora con el fin de controlar su producción. Se sabe que, a lo largo de un año la tasa de enfermos que necesitan este medicamento es de 5 personas en promedio.
¿Cuál es la probabilidad de que el número de enfermos no exceda 4 por año?
¿Cuál es la probabilidad de que el número de enfermos sea más de 2 por año?
¿Cuál es la probabilidad de que el número de enfermos sea de 3 a 6 por año?
1.3 Variables aleatorias continuas (v.a.c)
Una variable aleatoria continua tiene una probabilidad 0 de adoptar exactamente cualquiera de sus valores. En consecuencia, su distribución de probabilidad no se puede presentar en forma tabular. En un principio esto parecería sorprendente, pero se vuelve más probable cuando consideramos un ejemplo específi co. Consideremos una variable aleatoria cuyos valores son las estaturas de todas las personas mayores de 21 años de edad. Entre cualesquiera dos valores, digamos 163.5 y 164.5 centímetros, o incluso entre 163.99 y 164.01 centímetros, hay un número infi nito de estaturas, una de las cuales es 164 centímetros. La probabilidad de seleccionar al azar a una persona que tenga exactamente 164 centímetros de estatura en lugar de una del conjunto infi nitamente grande de estaturas tan cercanas a 164 centímetros que humanamente no sea posible medir la diferencia es remota, por consiguiente, asignamos una probabilidad 0 a tal evento.
Aunque la distribución de probabilidad de una variable aleatoria continua no se puede representar de forma tabular, sí es posible plantearla como una fórmula, la cual necesariamente será función de los valores numéricos de la variable aleatoria continua \(X\), y como tal se representará mediante la notación funcional \(f(x)\).
1.3.1 Función de densidad de probabilidad
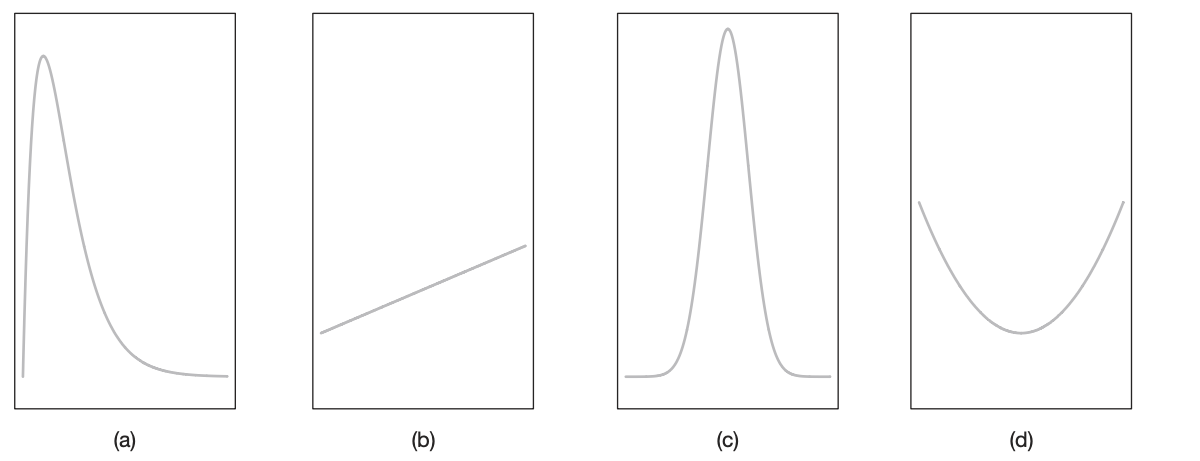
Cuando se trata con variables continuas, a \(f(x)\) por lo general se le llama función de densidad de probabilidad, o simplemente función de densidad de \(X\). Como \(X\) se define sobre un espacio muestral continuo, es posible que \(f(x)\) tenga un número finito de discontinuidades. Sin embargo, la mayoría de las funciones de densidad que tienen aplicaciones prácticas en el análisis de datos estadísticos son continuas y sus gráficas pueden tomar cualesquiera de varias formas, algunas de las cuales se presentan en la grafica siguiente grafica. Como se utilizarán áreas para representar probabilidades y éstas son valores numéricos positivos, la función de densidad debe caer completamente arriba del eje \(x\). (Walpole., 2012f, página 88)
Si se mide la profundidad con mucho más precisión y se utiliza el mismo eje de medición de la figura a), cada rectángulo en el histograma de probabilidad resultante es mucho más angosto, aun cuando el área total de todos los rectángulos sigue siendo 1. En la figura b) se ilustra un posible histograma; tiene una apariencia mucho más regular que el histograma de la figura a). Si se continúa de esta manera midiendo la profundidad más y más finamente, la secuencia resultante de histogramas se aproxima a una curva más regular, tal como la ilustrada en la figura c). Como en cada histograma el área total de todos los rectángulos es igual a 1, el área total bajo la curva regular también es 1. La probabilidad de que la profundidad en un punto seleccionado al azar se encuentre entre \(a\) y \(b\) es simplemente el área bajo la curva regular entre \(a\) y \(b\). Es de manera exacta una curva regular del tipo ilustrado en la figura c) la que especifica un distribución de probabilidad continua
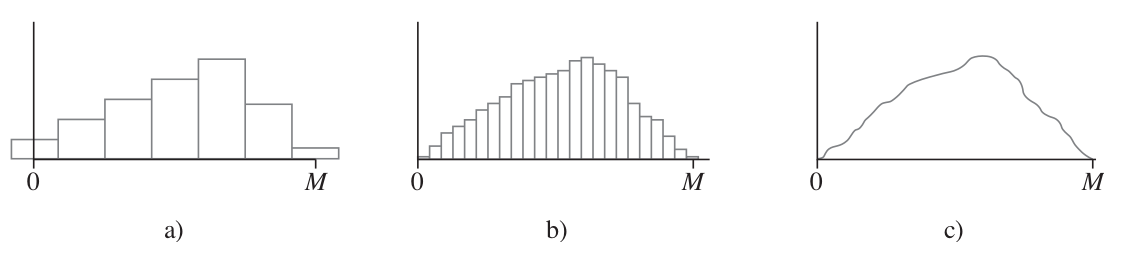
Una función de densidad de probabilidad se construye de manera que el área bajo su curva limitada por el eje x sea igual a 1, cuando se calcula en el rango de \(X\) para el que se define \(f(x)\). Como este rango de \(X\) es un intervalo finito, siempre es posible extender el intervalo para que incluya a todo el conjunto de números reales definiendo \(f(x)\) como cero en todos los puntos de las partes extendidas del intervalo.
En la siguiente grafica se observa la probabilidad de que \(X\) tome un valor entre \(a\) y \(b\) es igual al área sombreada bajo la función de densidad entre las ordenadas en \(x = a\) y \(x = b\), y a partir del cálculo integral está dada por
\[P(a\leq X\leq b) = \int_a^b f(x)dx\]
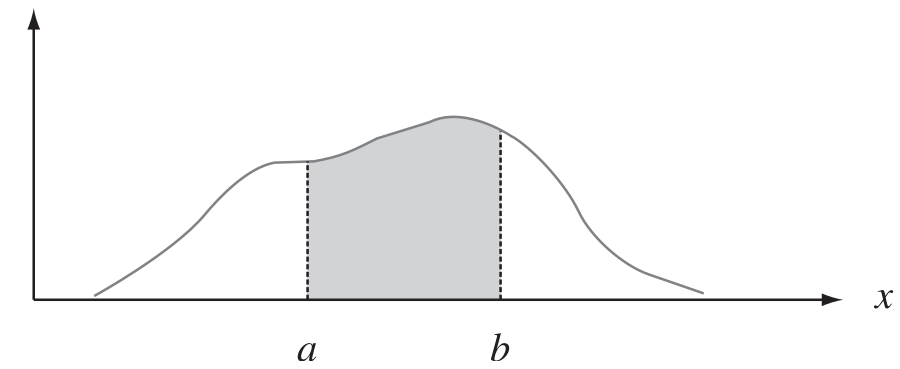
La función \(f(x)\) es una función de densidad de probabilidad (fdp) para la variable aleatoria continua \(X\), definida en el conjunto de números reales, si cumple las siguientes condiciones
- \(f(x) \geq 0, \forall x\)
- \(\displaystyle\int_{-\infty}^{\infty} f(x)dx = 1\)
Ejemplo: “Intervalo de tiempo” en el flujo de tránsito es el tiempo transcurrido entre el tiempo en que un carro termina de pasar por un punto fijo y el instante en que el siguiente carro comienza a pasar por ese punto. Sea \(X=\) el intervalo de tiempo de dos carros consecutivos seleccionados al azar en una autopista durante un periodo de tráfico intenso. La siguiente función de densidad de probabilidad de X es en esencia el sugerido en “The Statistical Properties of Freeway Traffic” (Transp. Res. vol. 11: 221-228):
\[f(x) = 0.15e^{-0.15(x-0.5)} \text{, } x \geq 0.5\]
\(\text{Ayuda : } \int_a^{\infty}e^{-kx}dx = \frac{1}{k}e^{-ka}\)
Verificar si es \(f(x)\) es función de densidad.
Condición 01:
fdp = function(x){
f = 0.15*exp(-0.15*(x-0.5)) # Expresión de la función de densidad
return(f)
}
x = seq(0.5, 10, by = 0.01) # Valores del dominio
f = fdp(x) # Valores del recorrido
df = data.frame("x" = x, "f" = f) # Data frame para poder usar ggplot
library(ggplot2)
ggplot(data = df, aes(x = x, y = f)) + geom_line() +
labs(title = "Función de densidad", x = "Valores de X", y = "f(x)")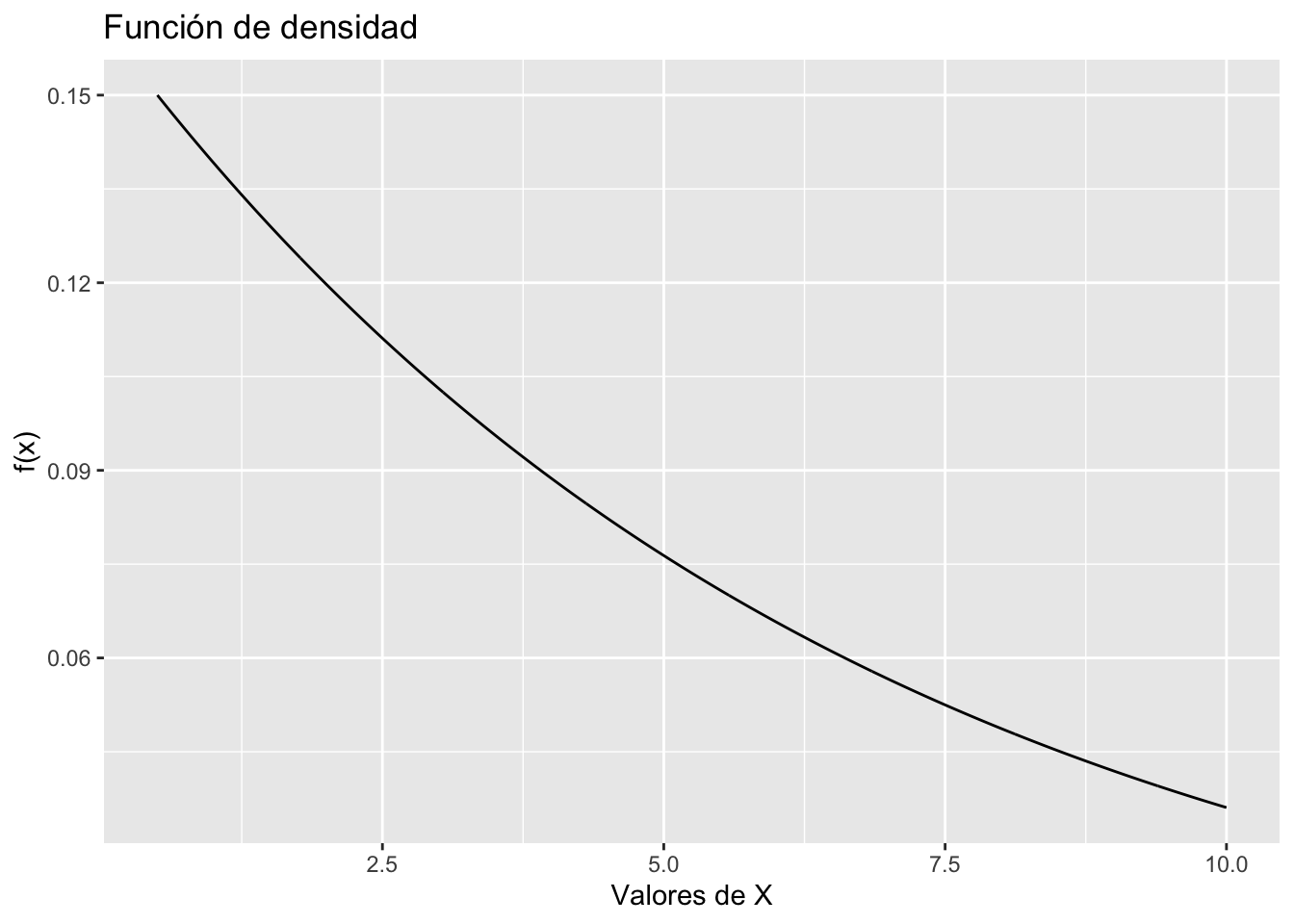
Condición 02:
\[\begin{equation} \notag \begin{split} \int_{-\infty}^{\infty} f(x)dx &= \int_{0.5}^{\infty} 0.15e^{-0.15(x-0.5)}dx = 0.15e^{0.075}\int_{0.5}^{\infty} e^{-0.15x}dx\\ &= 0.15e^{0.075}\frac{1}{0.15}e^{-0.075} = 1 \end{split} \end{equation}\]
## 1 with absolute error < 8e-06Así, la probabilidad de que el intervalo de tiempo sea cuando mucho de 5 segundos es
\[\begin{equation} \notag \begin{split} P(X\leq 5) &= \int_{-\infty}^{5} f(x)dx = \int_{0.5}^{5} 0.15e^{-0.15(x-0.5)}dx\\ &= 0.15e^{0.075}\int_{0.5}^{5} e^{-0.15x}dx = \left. 0.15e^{0.075}\frac{-1}{0.15}e^{-0.15x}\right|_{x = 0.5}^{x = 5}\\ &= e^{0.075}\left(e^{-0.75} + e^{-0.075} \right) = 1.078(-0.472 + 0.928) = 0.491\\ \end{split} \end{equation}\]
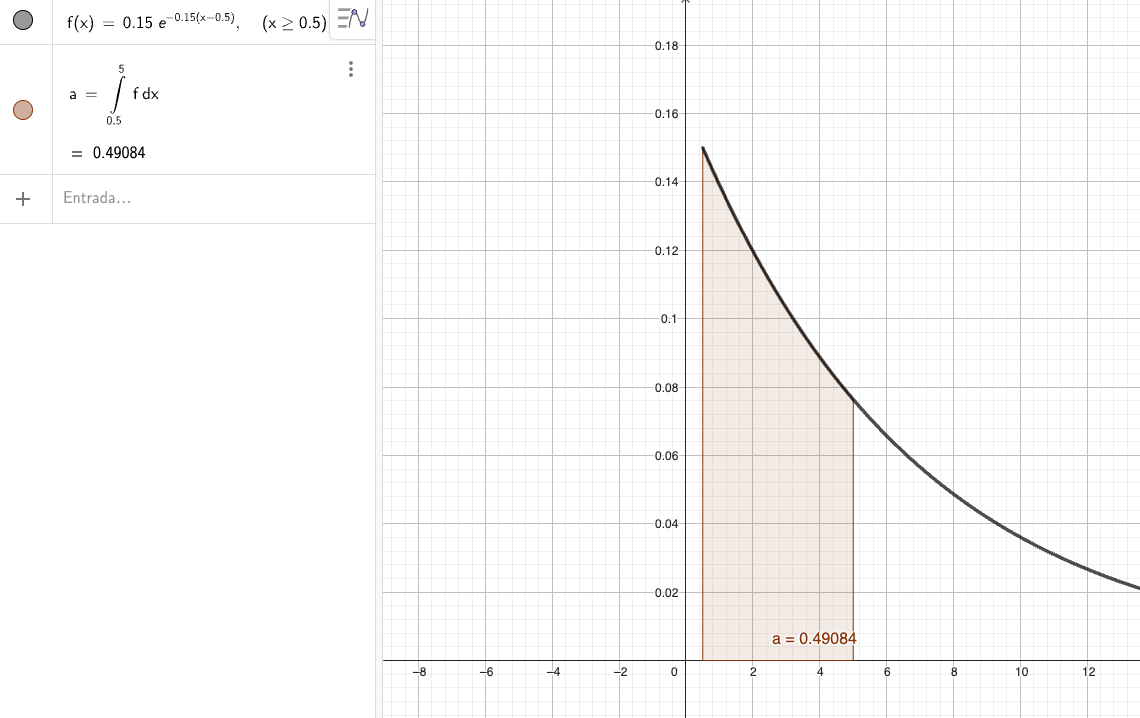
En R para hacer el cálculo de la integral es posible utilizar el comando integrate:
## 0.4908436 with absolute error < 5.4e-15- Usando GeoGebra, con el comando Integral
Ejercicio: Sea \(X\) la cantidad de tiempo durante la cual un libro puesto en reserva durante dos horas en la biblioteca de una universidad es solicitado en préstamo por un estudiante. Suponga que \(X\) tiene la siguiente función de densidad
\[f(x) = 0.5x \text{, } 0\leq x \leq 2\]
Calcule las siguientes probabilidades (manualmente o con algún programa)
- \(P(X \leq 1)\)
- \(P(0.5 \leq X \leq 1.5)\)
- \(P(1.5 < X)\)
Ejercicio: El error implicado al hacer una medición geográfica computarizada es una variable aleatoria continua \(X\) con función de densidad de probabilidad
\[f(x) = 0.09375(4-x^2) \text{, } -2\leq x \leq 2\] a. Bosqueje la gráfica de \(f(x)\)
Calcule \(P(X>0)\).
Calcule \(P(-1 < X < 1)\)
Calcule \(P(X<0.5\,\,o\,\, X>0.5)\)
Ejercicio: Un profesor universitario nunca termina su disertación antes del final de la hora y siempre termina dentro de 2 minutos después. Sea \(X=\) el tiempo que transcurre entre el final de la hora y el final de la disertación y suponga que la función de densidad de probabilidad de \(X\) es
\[f(x) = kx^2 \text{, } 0\leq x \leq 2\]
Determine el valor de \(k\) y trace en R la curva de densidad correspondiente.
¿Cuál es la probabilidad de que la disertación termine dentro de un minuto del final de la hora?
¿Cuál es la probabilidad de que la disertación continúe después de la hora durante entre 60 y 90 segundos.
¿Cuál es la probabilidad de que la disertación continúe durante por lo menos 90 segundos después del final de la hora?
1.3.2 Función de distribución acumulada
La función de distribución acumulativa (acumulada) \(F(x)\), de una variable aleatoria continua \(X\) con función de densidad \(f(x)\), es
\[F(x) =P(X\leq x) = \int_{-\infty}^xf(y)dy\]
Como una consecuencia inmediata de la definición anterior se pueden escribir los dos resultados,
\[P(a\leq X\leq b)= F(b)-F(a) \,\, y \,\, f(x)=\dfrac{dF(x)}{dx}\text{ , si existe la derivada.}\]
Con cada \(x\) , \(F(x)\) es el área bajo la curva de densidad a la izquierda de \(x\). Esto se ilustra en la siguiente figura, donde \(F(x)\) se incrementa con regularidad a medida que \(x\) se incrementa.
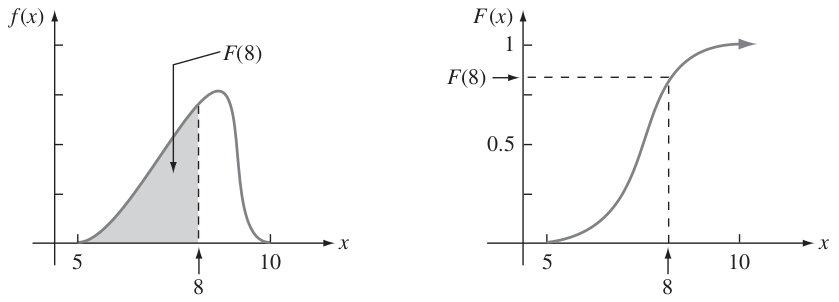
Ejemplo: Suponga que la función de densidad de probabilidad de la magnitud \(X\) de una carga dinámica sobre un puente (en newtons) está dada por
\[\begin{equation} \notag f(x) = \left\lbrace \begin{matrix} \displaystyle\frac{1}{8} + \displaystyle\frac{3}{8}x & 0\leq x \leq 2 \\ 0 & \text{en otro caso} \end{matrix} \right. \end{equation}\]
Determine función de distribución acumulativa (acumulada) \(F(x)\)
\[\begin{equation} \notag F(x) = \int_{-\infty}^xf(y)dy = \int_{0}^x \left(\frac{1}{8} + \frac{3}{8}y\right) dy = \frac{x}{8} + \frac{3}{16}x^2 \end{equation}\]
Por lo tanto queda,
\[\begin{equation} \notag F(x) = \left\lbrace \begin{matrix} 0 & x<0 \\ \displaystyle\frac{x}{8} + \displaystyle\frac{3}{16}x^2 & 0\leq x \leq 2 \\ 1 & x > 2\\ \end{matrix} \right. \end{equation}\]
La importancia de la función de distribución acumulada en este caso, lo mismo que para variables aleatorias discretas, es que las probabilidades de varios intervalos pueden ser calculadas con una fórmula o una tabla de \(F(x)\). En el caso de una variable aleatoria continua \(X\) con función de densidad de probabilidad \(f(x)\) y función de distribución acumulada \(F(x)\), se tiene que con cualquier número
\(a\),
\[P(X>a) = 1 - F(a)\]
y para dos números cualesquiera \(a\) y \(b\) con \(a<b\).
\[P(a\leq X \leq b) = F(b) - F(a)\]
La siguiente figura representa la probabilidad bajo la curva de densidad entre \(a\) y \(b\), (área sombreada ). Esto es diferente para una variable aleatoria discreta.

Continuando con el ejemplo anterior, la probabilidad de que la carga esté entre 1 y 1.5 es
\[P(1 \leq X \leq 1.5) = F(1.5) - F(1)\]
Utilizando la función del gráfico para la función de distribución acumulada, el resultado es
densidad = function(x){ # Función de densidad
return(1/8+3/8*x)
}
acumulada = function(x){ # Función de distribución acumulada
return(x/8+3/16*x^2)
}## [1] 0.296875Obsevando graficas
df = data.frame("x" = seq(0,2,0.01), # Valores de X
"fx" = densidad(seq(0,2,0.01)), # Valores de la densidad
"Fx" = acumulada(seq(0,2,0.01))) # Valores acumulados
# Gráfico de línes de ambas funciones
ggplot(data = df) +
geom_line(aes(x = x, y = fx, color = "Densidad")) +
geom_line(aes(x = x, y = Fx, color = "Acumulada")) +
labs(color = "Función", x = "Valores de X", y = "")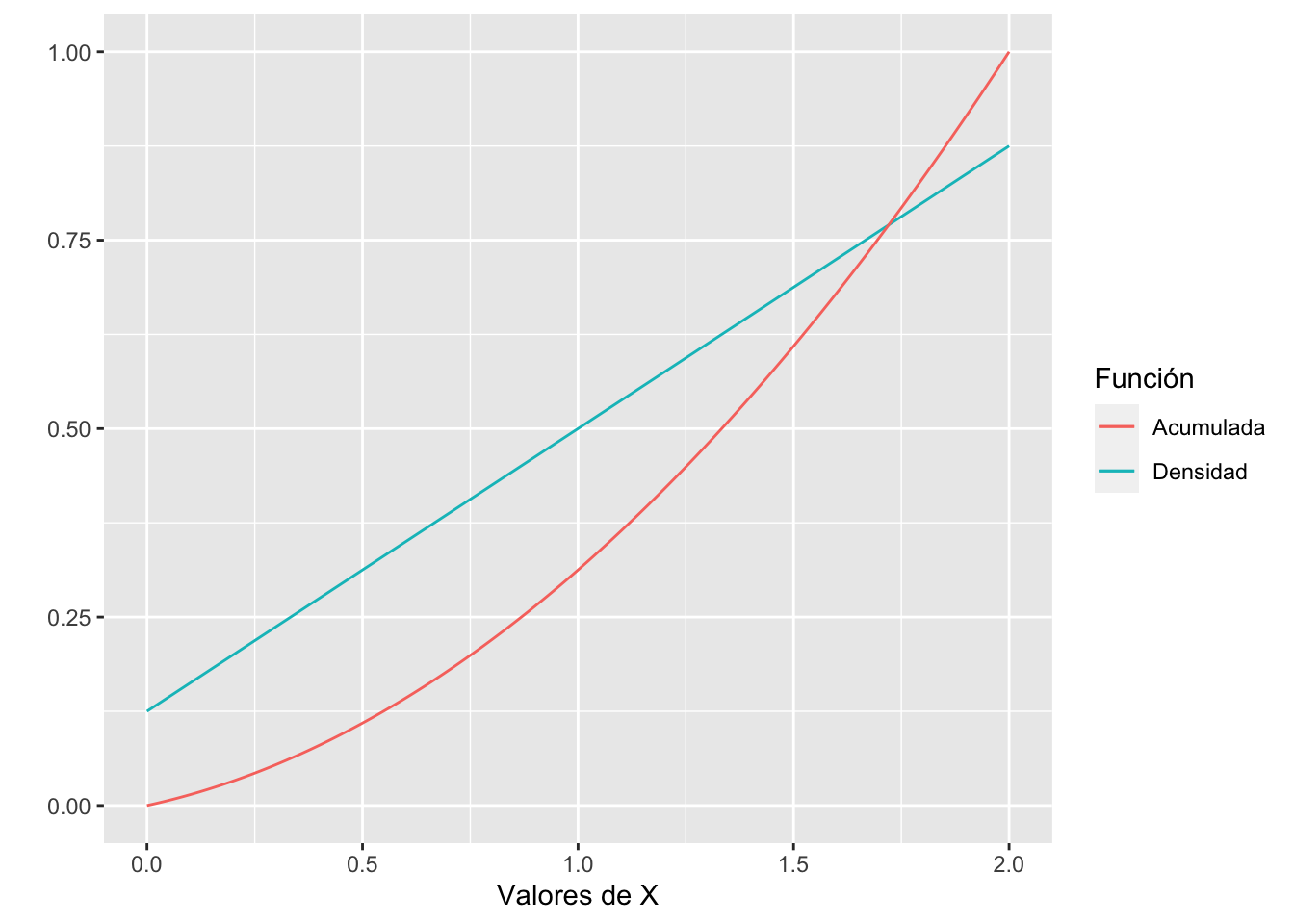
Ejercicio 01: Sea \(X\) la cantidad de tiempo durante la cual un libro puesto en reserva durante dos horas en la biblioteca de una universidad es solicitado en préstamo por un estudiante seleccionado. La función de distribución acumulativa del tiempo de préstamo \(X\) es
\[\begin{equation} \notag F(x) = \left\lbrace \begin{matrix} 0 & x<0 \\ \displaystyle\frac{x^2}{4} & 0\leq x < 2 \\ 1 & x \geq 2\\ \end{matrix} \right. \end{equation}\]
Determine
\(P(X≤1)\)
\(P(0.5≤X≤1)\)
\(P(X>0.5)\)
\(f(x)\)
Grafique \(f(x)\) y \(F(x)\).
Ejercicio 02: El error de medición de un proceso de control de gestión en la peligrosidad de residuos está dado por la siguiente función de distribución acumulada.
\[\begin{equation} \notag F(x) = \left\lbrace \begin{matrix} 0 & x < -2 \\ \displaystyle\frac{1}{2} + \displaystyle\frac{3}{32}\left(4x-\displaystyle\frac{x^3}{3}\right) & -2\leq x < 2 \\ 1 & x \geq 2\\ \end{matrix} \right. \end{equation}\]
Determine
\(P(X<0)\)
\(P(-1≤X≤1)\)
\(P(0.5<X)\)
\(f(x)\)
Grafique \(f(x)\) y \(F(x)\).
Ejercicio 03: En un ejemplo anterior se uso el pto de intervalo de tiempo en el flujo de tránsito y propuso una distribución particular para \(X=\) el intervalo de tiempo entre dos carros consecutivos seleccionados al azar (s). Suponga que en un entorno de tránsito diferente, la distribución del intervalo de tiempo tiene la forma
\[\begin{equation} \notag f(x) = \left\lbrace \begin{matrix} \displaystyle\frac{k}{x^4} & x > 1 \\ 0 & x \leq 1\\ \end{matrix} \right. \end{equation}\]
Determine el valor de \(k\) con el cual \(f(x)\) es una función de densidad de probabilidad legítima.
Obtenga la función de distribución acumulada.
Use la función de distribución acumulada de \((b)\) para determinar la probabilidad de que el intervalo de tiempo exceda de 2 segundos y también la probabilidad de que el intervalo esté entre 2 y 3 segundos.
Grafique la función de densidad de probabilidad y la función de distribución acumulada.
1.3.3 Distribuciones
A continuación, se dan a conocer algunas de las distribución de probabilidad continua más utilizadas. Cabe mencionar, que existen muchas otras distribuciones.
1.3.3.1 Uniforme
La función de probabilidad asociada es:
\[\begin{equation} \notag f(x) = \left\lbrace \begin{array}{cl} \displaystyle\frac{1}{b-a} & \text{si } x \in (a,b)\\ 0 & \text{si } x \not\in (a,b) \end{array} \right. \end{equation}\]
Notación: \(U(a,b)\)
Ejemplo: Imagine que eres un analista financiero encargado de los rendimientos diarios de una acción en particular en el mercado de valores. Los rendimientos diarios de esta acción se distribuyen de manera uniforme continua entre -2% y 2%, es decir, \(U(a = -2, b = 2)\).
En este caso, la distribución uniforme continua significa que cada valor dentro del rango dado tiene la misma probabilidad de ocurrir. Por lo tanto, la probabilidad de que el rendimiento diario de la acción sea cualquier valor entre −2% y 2% es igual.
Supongamos que estás interesado en calcular la probabilidad de que el rendimiento diario de la acción sea mayor o igual a 1.2% (Resp. \(P(X\geq 1.2\%) = 0.2)\)
1.3.3.2 Exponencial
Esta es una de las pocas variables aleatorias continuas que se aplica a un contexto de determinado. Se utiliza para modelar tiempos de espera para la ocurrencia de un determinado evento (éxito). ¿Qué similitudes y diferencias tiene con la variable discreta Poisson?.
La función de densidad asociada es:
\[\begin{equation} \notag f(x)= \left\lbrace \begin{array}{cl} \lambda e^{ -\lambda x} & \text{si } x \geq 0\\ 0 & \text{si } x < 0 \end{array} \right. \end{equation}\]
con \(λ>0\). ¿Qué interpretación tiene lambda?
Notación: \(Exp(λ)\)
Ejemplo: Se está analizando el tiempo de espera de los clientes en una tienda y se desea calcular la probabilidad de que un cliente tenga que esperar más de 15 minutos antes de ser atendido. Suponiendo que el tiempo promedio de espera es de 10 minutos, es posible utilizar la distribución exponencial para calcular esta probabilidad.
Lambda se calcula como el recíproco del tiempo promedio, es decir, \(λ=\dfrac{1}{10}\). Luego, se desea calcular
\[P(X > 15)\]
## [1] 0.2231302- Usando GeoGebra:
- Usando Excel
Ejercicios
Un componente eléctrico tiene una vida útil media de 8 años. Si su vida útil se distribuye en forma exponencial. ¿Cuál debe ser el tiempo \(x\) de garantía que se debe otorgar, si se desea reemplazar a lo más el 15% de los componentes que fallen dentro de este período?
Las personas que solicitan créditos en un banco son sometidas a un estudio de morosidad. En general, el tiempo promedio de una persona para volverse morosa es de 4 años después de solicitar un crédito. Si el momento en que una persona se vuelve morosa distribuye de forma exponencial con \(x\) en años, ¿cuál es la probabilidad de que una persona se vuelva morosa posterior al quinto año después de solicitar un crédito?
Las personas que solicitan créditos en un banco son sometidas a un estudio de morosidad. En general, el tiempo promedio de una persona para volverse morosa es de 4 años después de solicitar un crédito. Si el momento en que una persona se vuelve morosa distribuye de forma exponencial con \(x\) en años, ¿cuál es la probabilidad de que una persona se vuelva morosa posterior al quinto año después de solicitar un crédito?
1.3.3.3 Normal
Esta es una de la variables continuas más usadas. Lamentablemente, no existe un característica fenomenológica que permita deducir cuando es adecuado utilizar esta variable. La función de desindad de probabilidad asociada es la siguiente.
\[\begin{equation} \notag f(x)= (2\pi \sigma^2)^{-1/2}e^{\left( -\displaystyle\frac{(x-\mu)^2}{2\sigma^2} \right)} ,x \in R \end{equation}\]
Notación: \(N(μ,σ^2)\)
Estándarizar:
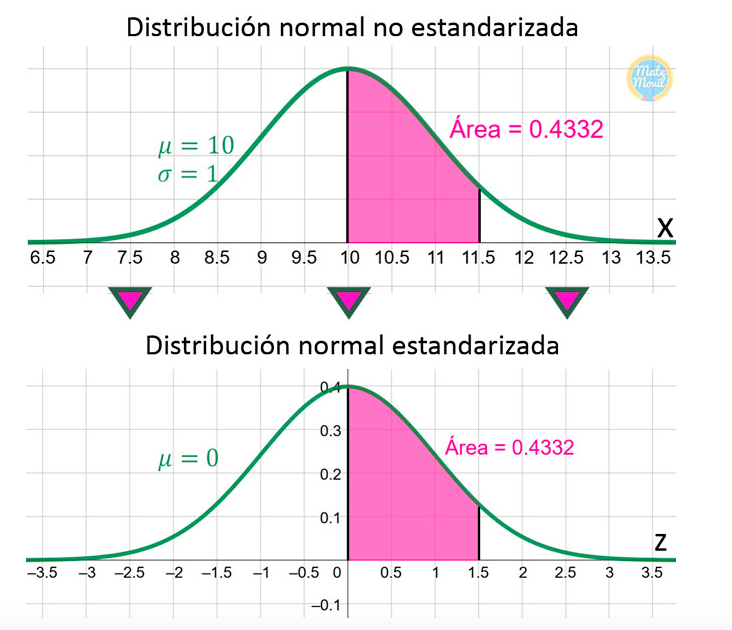
\[Z=\dfrac{X-\mu}{\sigma}\]
Se está analizando los ingresos mensuales de una empresa y se desea calcular la probabilidad de que los ingresos estén por debajo de \(\$6000\) miles de dólares. Además, se sabe que los ingresos mensuales siguen una distribución normal con una media de \(\$5000\) (miles de dólares )y una desviación estándar de \(\$1000\) (miles de dólares). La probabilidad a calcular es \(P(X<6000)\) .
## [1] 0.8413447Ejercicios:
En un bar se ha instalado una máquina automática para la venta de cervezas. La máquina puede regularse de modo que la cantidad media de cerveza por vaso sea la que se desea. Además, se sabe que el proceso de llenado sigue una distribución normal, y que independiente de la cantidad a llenar la desviación estándar es 5.9 ml. Si el nivel medio se ajusta a 304.6 ml determine qué porcentaje de los vasos contendrá menos de 295.7ml.
Cada cierto periodo de tiempo, el Banco Central de Chile realiza una inyección de capital al mercado chileno, con el fin de mermar el efecto de la inflación. El dinero que destina el banco, sigue un distribución normal con media 15 (miles de millones) y una varianza de 4 (miles de millones). ¿Cuál es probabilidad el banco inyecte más de 15.6 miles de millones de pesos?
La mayoría de las transacciones electrónicas en Chile están a cargo de la empresa Transbank. Además, se sabe que la cantidad de transacciones realizadas por Transbank sigue un distribución normal con una media de 20 millones.
- Si la varianza de las transacciones es de 25 millones, ¿cuál es la probabilidad de que Transbank esté a cargo de más de 30 millones de transacciones?
- Si la varianza de las transacciones es de 16 millones, ¿cuántas deben ser las transacciones para que la probabilidad de que Transbank se haga cargo de un número mayor sea de un 34%?
- El tipo de cambio del euro ha fluctuado de manera similar al dólar en los últimos 4 años. Si valor observado del euro sigue un distribución normal con media \(\$912\) y varianza \(\$144\).
¿Cuál es la probabilidad de que el tipo de cambio del euro supere los \(\$920\)?
¿A cuánto debe estar el tipo de cambio para que la probabilidad de que el euro supere ese valor sea de un 21.9%?
- Los residuos de vuelo de una determinad aerolínea son recolectados al final de cada semana, generando en promedio 48 toneladas de residuos. Además, la cantidad de residuos generados por los vuelos sigue una distribución normal.
Si la varianza de los residuos generados es de 100, ¿cuál es la probabilidad de que la aerolínea genere más de 50 toneladas de residuos?
Si la varianza de los residuos generados es de 120, ¿cuántos deben ser los residuos para que la probabilidad de que la aerolínea genere menos sea de un 87%?
- El sistema logístico de lavado de autos de una determinada empresa ha optado por instalar una máquina automática para la atención de clientes. Se sabe que la cantidad de clientes que son atendidos por la máquina sigue una distribución normal con una varianza de 90 personas.
Si el promedio de personas atendidas por la máquina es de 390, ¿cuál es la probabilidad de que la máquina atienda a menos de 385 personas?
Si el promedio de personas atendidas por la máquina son de 360, ¿cuántas personas como mínimo que deben ir a la máquina para que la posibilidad de que sean atendidas sea de un 70%?
1.4 Esperanza y Varianza
Esperanza \(\mathbb{E}(X)\)
Se \(X\) una variable aleatoria discreta o continua con función de probabilidad \(px\) o \(fx\) respectivamente, el valor esperado de \(X\) o esperanza, se define como
\[\begin{equation} \notag \mathbb{E}(X)= \left\lbrace \begin{array}{cl} \displaystyle\sum_{x\,\in\, R_{x}}x\cdot p(x) & \text{si X es Discreta }\\ \displaystyle\int_{x\,\in\, R_{x}}x\cdot f(x) dx & \text{si X es Continua } \end{array} \right. \end{equation}\]
Varianza \(\mathbb{V}(X)\)
Forma abreviada: \(\mathbb{V}(X)= \mathbb{E}(X^2)-[\mathbb{E}(X)]^2\)
Desviación Estándar de \(X\) es \(\sigma_x=\sqrt{\mathbb{V}(X)}\)
\(\Large{\text{Casos particulares}}\)
- Distribución Binomial:
\(\mathbb{E}(X) = n\cdot p\)
\(\mathbb{V}(X) = n\cdot p \cdot q\)
- Distribución Poisson:
\(\mathbb{E}(X) = \lambda\)
\(\mathbb{V}(X) = \lambda\)
- Distribución Uniforme:
\(\mathbb{E}(X) = \dfrac{a+b}{12}\)
\(\mathbb{V}(X) = \dfrac{(b-a)^2}{2}\)
- Distribución Exponencial:
\(\mathbb{E}(X) = \dfrac{1}{\lambda}\)
\(\mathbb{V}(X) =\dfrac{1}{\lambda^2}\)