Unidad 3 Intervalos de confianza

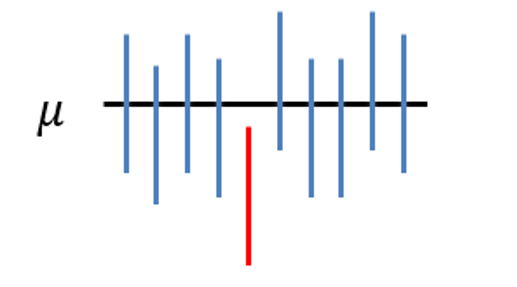
Dado que los estimadores puntuales raramente coincidirán con los parámetros que tratan de estimar, es posible otorgarse un mayor libertad en su estimación mediante el uso de la “estimación por intervalos” o “intervalos de confianza”. Un intervalo de confianza es un intervalo dentro del cual se espera encontrar el verdadero valor de un parámetro.

Definición: Sea \(1-α\) una probabilidad especificada alta y sean \(T_1\) y \(T_2\), dos estadísticos tales que:

\[\begin{equation} P\left( T_{1} < \hat{\theta} < T_{2}\right) = 1-\alpha \end{equation}\]

El intervalo \([T_1, T_2]\) recibe el nombre de Intervalo de Confianza del \(100(1-α)\)% para el parámetro desconocido \(θ\). Las cantidades \(T_1\), \(T_2\) reciben el nombre de límites de confianza inferior y superior, respectivamente, y \((1-α)\) es el Nivel de Confianza asociado con el intervalo.

La interpretación de un intervalo de confianza radica, en la interpretación de una probabilidad de largo plazo, y es que, si se recopila un número grande de muestras aleatorias y se calcula un intervalo de confianza del \(100(1-α)\)% para el parámetro \(θ\) para cada una de las muestras, entonces el \(100(1- α)\)% de esos intervalos contienen el valor verdadero de \(θ\).

Observación 01: Es fundamental para calcular un intervalo de confianza determinar el valor de \(𝛼\) a partir del nivel de confianza.

Ejemplos:

Un intervalo de confianza del 99% implica que \(𝛼=0,01\).
Un intervalo de confianza del 98% implica que \(𝛼=0,02\).
Un intervalo de confianza del 95% implica que \(𝛼=0,05\).
Un intervalo de confianza del 90% implica que \(𝛼=0,1\).

El nivel de confianza representa el porcentaje de intervalos que incluyen el parámetro si se toman varias muestras de la misma población

Observación 02: A mayor nivel de confianza de un intervalo, mayor amplitud, lo que implica una menor precisión.

Observación 03: A menor nivel de confianza de un intervalo, menor amplitud, lo que implica una mayor precisión.

Elaboración:

Se tiene una muestra \(n\), cuya la media muestral \(X\) está normalmente distribuida con valor esperado \(μ\) y desviación estándar \(\dfrac{σ}{\sqrt{n}}\). Si se estandariza el promedio se obtiene la variable normal estándar.

\[\begin{equation} Z = \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim N(\mu = 0,\sigma^2=1) \tag{1.1} \end{equation}\]

Luego, en caso de estar interesado en construir un intervalo (bilateral) de confianza para la media con una determinada confianza, se debe plantear de la siguiente forma:

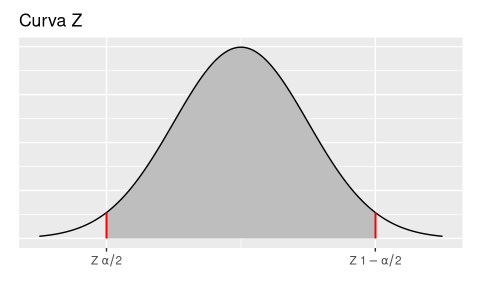
\[\begin{equation} P\left( Z_{\alpha/2} < Z < Z_{1-\alpha/2}\right) = 1-\alpha \tag{1.2} \end{equation}\]

\(Z_{\alpha/2} = x : P(X \leq x) = \alpha/2\)

\(Z_{1-\alpha/2} = x : P(X \leq x) = 1-\alpha/2\)

Luego, reemplazando el valor de \(Z\) por (1.1) en la ecuación (1.2), y despejando el valor \(μ\) al interior de la probabilidad, se obtiene la siguiente expresión.

\[\begin{equation} P\left( \overline{X} + Z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + Z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right) = 1-\alpha \tag{1.3} \end{equation}\]

\[\begin{equation} P\left( \overline{X} - Z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + Z_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\right) = 1-\alpha \tag{1.4} \end{equation}\]

A continuación, se dan a conocer intervalos de confianza para estimar la media poblacional, la diferencia de medias poblacionales y la comparación de varianzas, omitiendo los procesos de construcción.

3.1 Intervalo de confianza para la media

3.1.1 Intervalo de confianza para la media de una distribución normal y varianza poblacional conocida

Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a<\mu<b)=1-\alpha\)	\(\left(\bar{x} \pm Z_{1-\alpha/2}\displaystyle\frac{\sigma}{\sqrt{n}}\right)\)

Ejemplo 1: Los datos que a continuación se dan son los pesos en gramos del contenido de 16 cajas de cereal que se seleccionaron de una proceso de llenado con el propósito de verificar el peso promedio: 506, 508, 499, 503, 504, 510, 497, 512, 514, 505, 493, 496, 506, 502, 509, 496. Si el peso de cada caja es una variable aleatoria normal con una desviación estándar \(σ=5g\), obtener el intervalo de confianza al 99% para la media de llenado de este proceso.

Nota: \(\bar{x}= 503.75\)

Dado que, no se especifica el tipo de intervalo, y que se está interesado es el estudiar la media del llenado de las cajas de cereal, corresponde elaborar un intervalo de confianza bilateral:

peso = c(506,508,499,503,504,510,497,512,
         514,505,493,496,506,502,509,496)
promedio = mean(peso)
L = promedio - qnorm(1-0.01/2)*5/sqrt(length(peso))
U = promedio + qnorm(1-0.01/2)*5/sqrt(length(peso))
c(L,U)

## [1] 500.5302 506.9698

El resultado indica que, la probabilidad de que el intervalo(500.5,506.9) (en gramos) contenga el valor de la media de llenado de las cajas es de 0.99.

Obtener los intervalos con las confianzas al 90% y 95% asociados al ejemplo 1.1. Comente las diferencias e interprete.

3.1.2 Intervalo de confianza para la media de una distribución normal y varianza poblacional desconocida

Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a<\mu<b)=1-\alpha\)	\(\left(\bar{x} \pm t_{1-\alpha/2,n-1}\displaystyle\frac{\sigma}{\sqrt{n}}\right)\)

Para resolver el ejemplo anterior considerando varianza poblacional desconocida, es posible utilizar el comando t.test() para obtener el intervalo de confianza.

\[\left(\bar{x} \pm t_{1-\alpha/2,n-1}\displaystyle\frac{S}{\sqrt{n}} \right)\]

peso = c(506,508,499,503,504,510,497,512,
         514,505,493,496,506,502,509,496)
t.test(x = peso, conf.level = 0.99, alternative = "two.sided")

## 
##  One Sample t-test
## 
## data:  peso
## t = 324.89, df = 15, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 99 percent confidence interval:
##  499.181 508.319
## sample estimates:
## mean of x 
##    503.75

En este sentido, se tiene una probabilidad de 0.99 de que el intervalo (499.1,508.3) contenga el valor de la media de llenado de las cajas de cereal.

3.1.3 Intervalo de confianza para la proporción

Tipo de intervalo	Probabilidad	Expresión del intervalo
Bilateral	\(P(a<P<b)=1-\alpha\)	\(\left(\hat{p} \pm Z_{1-\alpha/2}\sqrt{\dfrac{\hat{p}\cdot \hat{q}}{n}}\right)\)

Ejemplo:

Se ha hecho un estudio sobre la proporción de enfermos de cáncer de pulmón detectados en hospital que fuman, obteniéndose que de 123 enfermos 41 de ellos eran fumadores. Obtener un intervalo de confianza para dicha proporción. Estudiar si dicha proporción puede considerarse igual a la proporción de fumadores en la población si está es de un \(29\%\)