Unidad 2 Muestreo
Recordar:
Población: Conjunto de todas las unidades que poseen una característica en común y son de interés en un estudio estadístico. El tamaño de la población se denota por \(𝑁\).
Parámetro: Medida resumen que describe una característica de la población. Generalmente se denota por letras del alfabeto griego: \(𝜇\), \(𝜎\), \(𝑝\), \(𝜃\), \(𝛽\), \(𝛼\), etc
Muestra: Subconjunto de la población en estudio. El tamaño de la muestra se denota por \(n\).
Estadístico (También llamado estadística de prueba o estadígrafo): Medida resumen que describe una característica de la muestra. Es una fórmula que se calcula usando los datos de una muestra.
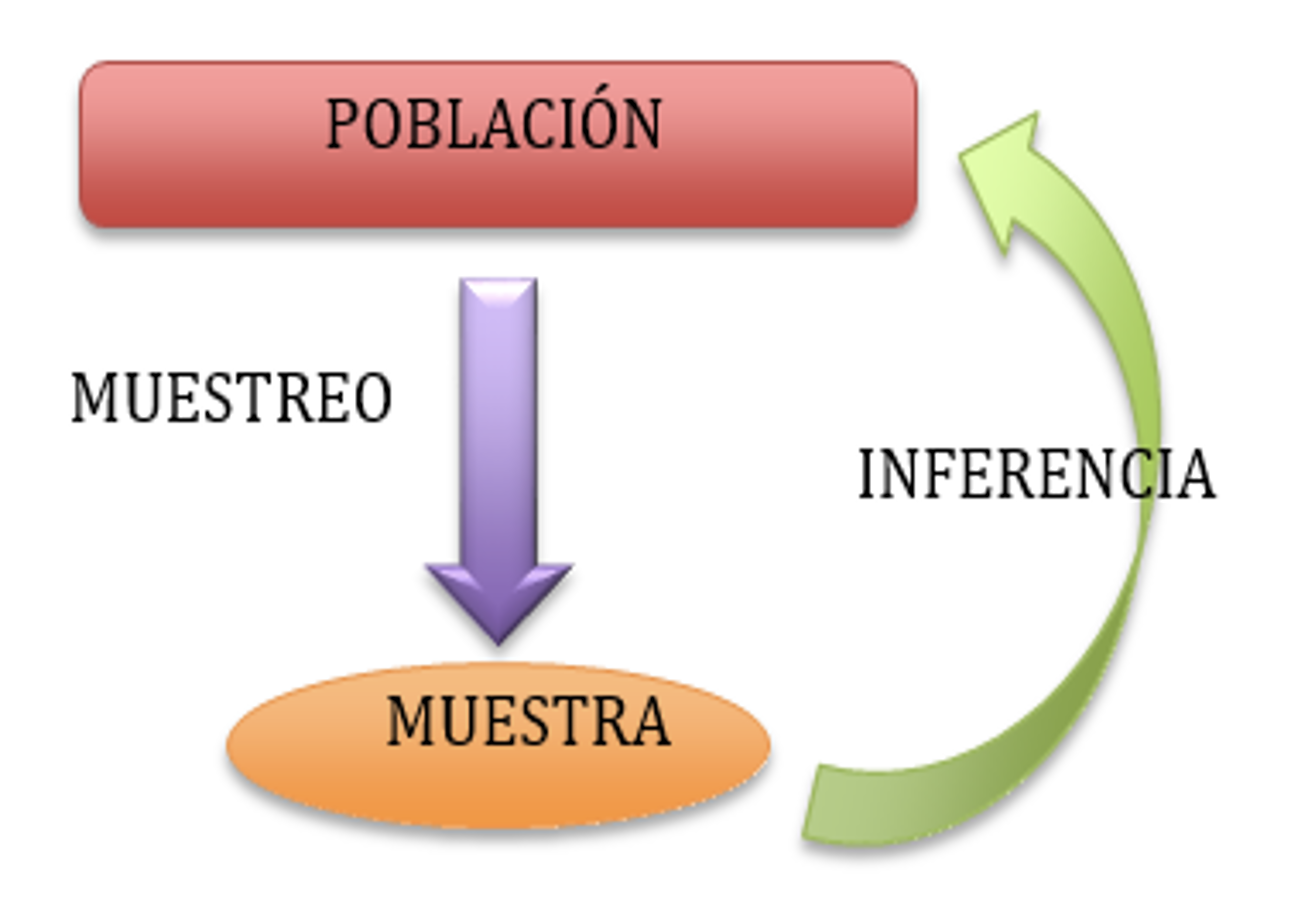
Inferencia estadística: Es un conjunto de métodos estadísticos que permiten predecir valores desconocidos de una población (parámetros) en base a los datos obtenidos en una muestra. Entre los métodos estadísticos más utilizados son la estimación de parámetros a través intervalos de confianza, dócimas de hipótesis y la regresión.
Muestreo: Conjunto de técnicas que permiten obtener una muestra a partir de una población.Existen los muestreos probabilísticos y los no probabilísticos.
2.1 Muestreos probabilisticos
Técnica de muestreo en la que los elementos de la población tiene una probabilidad conocidad de formar parte de la muestra. Estos son:
- Muestreo aleatorio simple (con y sin reemplazo)
- Muestreo aleatorio sistemático
- Muestreo Estratificado
- Muestreo por conglomerados
2.1.1 Muestreo Aleatorio simple:
En este tipo de muestreo todas las unidades de la población tienen la misma probabilidad de ser seleccionadas para formar parte de la muestra.
Existen dos tipos de muestreo aleatorio simple:
con reemplazo: cada elemento elegido se devuelve a la población, antes de hacer la siguiente selección. Formalmente coincide con el muestreo de poblaciones infinitas, ya que al devolver a la población cada elemento extraído de la misma, una vez anotadas sus características, la población es inagotable y el resultado de la extracción de cada elemento, es independiente de los anteriores él.
Sin reemplazo: el elemento que se selecciona para la muestra no se devuelve a la población, de tal forma que pierde su posibilidad de ser nuevamente seleccionado nuevamente.
2.1.2 Muestreo aleatorio sistemático:
Este método consiste en tomar los elementos de la población desde un listado o lista, de tal modo de poder seleccionar de \(k\) en \(k\) elementos, partiendo desde uno de ellos seleccionado aleatoriamente.
En primer lugar, se debe determina el entero más próximo al siguiente resultado: \(k=\dfrac{N}{n}\), el cual se llama salto sistemático (\(N\) es el tamaño de la población y \(n\) es el tamaño de la muestra). Luego se elige al azar un número m entre \(1\) y \(N\), para ser el primer seleccionado de la muestra, luego se avanza en la lista seleccionando los elementos \(m+k\), \(m+2k\), \(m+3k\)…. hasta completar \(n\) elementos de la muestra.
2.2 Muestreos no probabilisticos
La muestra se obtiene en función de ciertas caracteristicas que el investigador considere en un momento determinado. Esta información puede ser poco confiables para realizar inferencia.
Es importante mencionar por muy bien selecciondo e implementado el muestreo, es practicamente imposible que una muestra represente exactamente a la población. Esto quiere decir que siempre existirá una diferencia entre el valor estimado y el verdadero valor del parámetro. Esta diferencia es conocida como el error muestral. Una forma de controlar este error es aumentar el tamaño de la muestra, pero esto puede ser costoso y en algunos casos imposible.
2.3 Estimador
Son fórmulas que están en función de los datos de una muestra y que estiman el valor de los parámetros que caracterizan a la población. Si el parámetro se denota como \(θ\), entonces su estimador puntual se simboliza como \(\hat{\theta}\). Se llama puntual porque representa un solo valor numérico que se representa como un punto en la recta numérica. Los siguientes son algunos estimadores puntuales importantes; los de la media, la varianza, la desviación estándar y la proporción.
Ejercicios: (uso de calculadora)
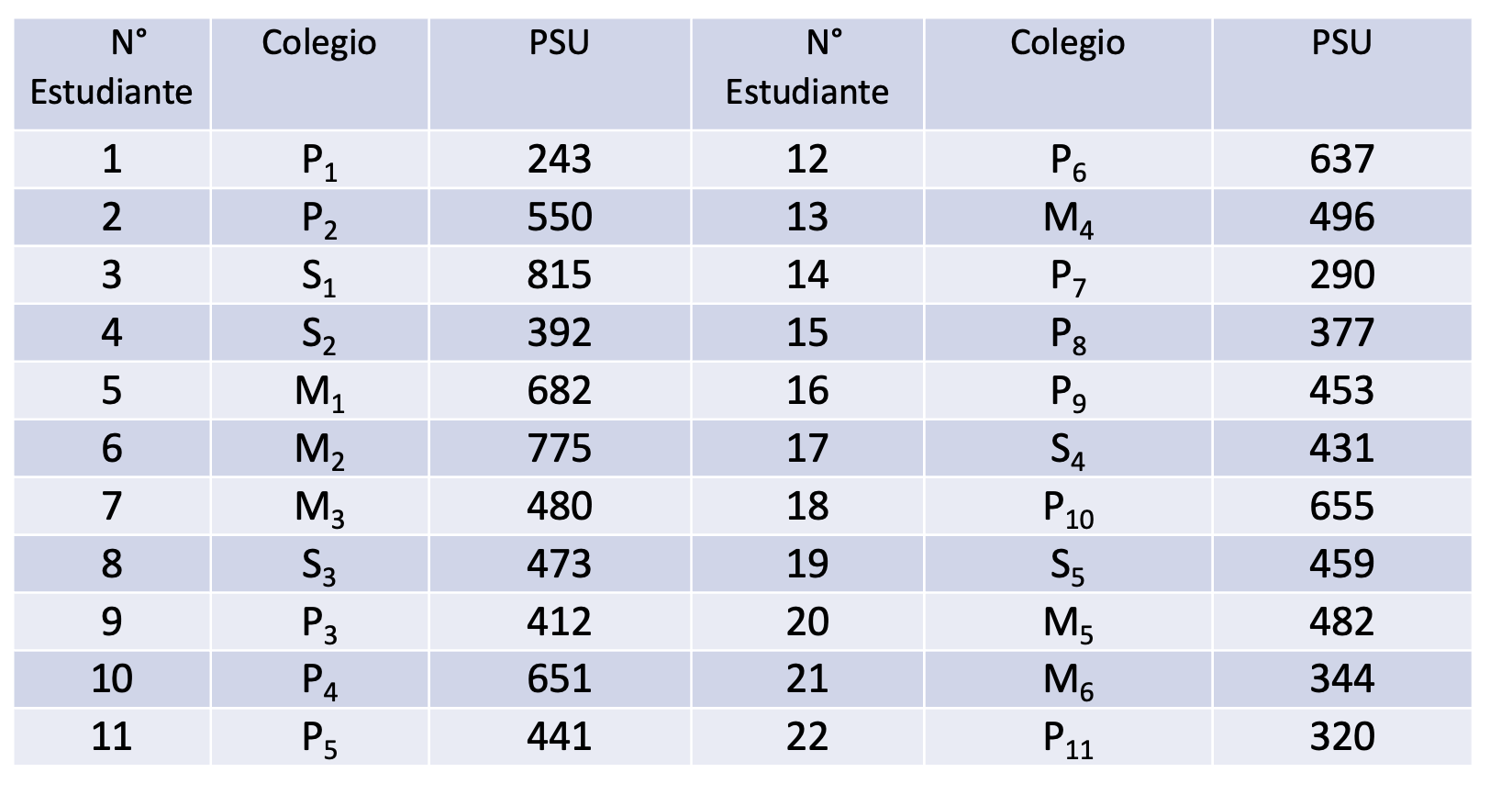
Se toma desde una base de datos (población) una muestra de 22 estudiantes de nuevo ingreso de una carrera. Se registraron las variables Tipo de colegio de egreso y Puntaje PSU. El tipo de colegio fue codificado de acuerdo en Municipal (M), Subvencionado(S) y particular pagado (P)
Ejercicio 1: Para este ejercicio se definirá la proporción \(𝒑\): proporción de estudiantes que obtienen más de 450 puntos. Responda las siguientes preguntas
- Tome una muestra aleatoria simple de tamaño 6 (con reemplazo) y calcule \(\bar{X}\),\(S^2\), \(S\) y \(\hat{p}\)
- Tome una muestra aleatoria simple de tamaño 6 (Sin reemplazo) y calcule \(\bar{X}\),\(S^2\), \(S\) y \(\hat{p}\)
- Tome una muestra de tamaño 6 usando un muestreo aleatorio sistemático. Considerando que para el inicio del muestreo se procedió a realizar un sorteo.Calcule \(\bar{X}\),\(S^2\), \(S\) y \(\hat{p}\)